Erfolgreich Bruchrechnen lernen in der Grundschule

Das Thema Brüche/ Bruchrechnen ist ein zentraler Bestandteil des Mathematikunterrichts, vor allem in der vierten Klasse. Obwohl das mathematische Konzept im Alltag allgegenwärtig ist, sei es beim Teilen eines Kuchens, beim Messen von Zutaten in der Küche oder beim Verstehen von Zeitangaben, ist das Thema für viele Kinder sehr schwer zu begreifen.

Umso mehr freue ich mich, dass bei mir ins Klassenzimmer das wunderbare Bruchrechnungs-Set von Höller Spiel eingezogen ist. Es besteht aus 2 Schichtenpuzzles, 20 Bruchwürfel, 20 Rechenzeichenwürfel und 20 Zahlenwürfel (1-6). Mit diesem Set kann man den Brüchen handelnd und mit anschaulichen Hilfsmitteln auf die Spur kommen und so ECHTES Verständnis erlangen. Wie genau, das zeig ich euch in folgendem Blogartikel:

Die Bedeutung des Bruchrechnens

Das Bruchrechnen ist ein grundlegender Teil der Mathematik und bildet die Basis für viele weiterführende mathematische Konzepte, wie Dezimalzahlen, Prozentrechnung und Algebra. Es hilft den Schülern, ein tieferes Verständnis für Zahlen und deren Teilbarkeit zu entwickeln. Zudem fördert es das logische Denken und die Fähigkeit, abstrakte Konzepte zu visualisieren. Das Verständnis für das Bruchrechnen ist also essenziell, um im weiterführenden Mathematikunterricht den Anschluss nicht zu verlieren.

Wie baue ich dieses Verständnis nun mit den SchülerInnen oder mit meinem Kind zu Hause auf? Ich verrate dir meine Methode:

Bruchrechnen leicht gemacht

Was ist ein Bruch?

Ein Bruch besteht aus zwei Teilen – dem Zähler (oben) und dem Nenner (unten). Der Zähler gibt an, wie viele Teile wir haben und der Nenner zeigt, in wie viele gleiche Teile das Ganze aufgeteilt ist. Zum Beispiel bedeutet der Bruch 3/4, dass wir drei von vier gleichen Teilen haben.

Dieses Verständnis erlangen die Kinder aber erst später im Lernprozess. Zuerst geht es darum, einen Bezug zur kindlichen Welt zu schaffen:

Einstieg ins Thema mit Alltagsbeispielen

Um den Schülern das Konzept der Brüche näherzubringen, ist es hilfreich, mit realen Beispielen zu arbeiten. Kuchenstücke, Pizzastücke oder Schokoladentafeln sind hervorragende visuelle Hilfsmittel, um zu zeigen, wie Brüche im täglichen Leben vorkommen. Beispielsweise kann man einen Apfel in Hälften, Viertel oder Achtel schneiden, um zu zeigen, wie aus einem Ganzen verschiedene Bruchteile entstehen.

Das Bruchrechnungs-Set von Höller Spiel eignet sich ebenso perfekt in dieser Phase. Die Kinder können sich mit den Bruchwürfeln vertraut machen, die einzelnen Teile zählen und diese den passenden Zahlenwürfeln und Puzzlestücken zuordnen.

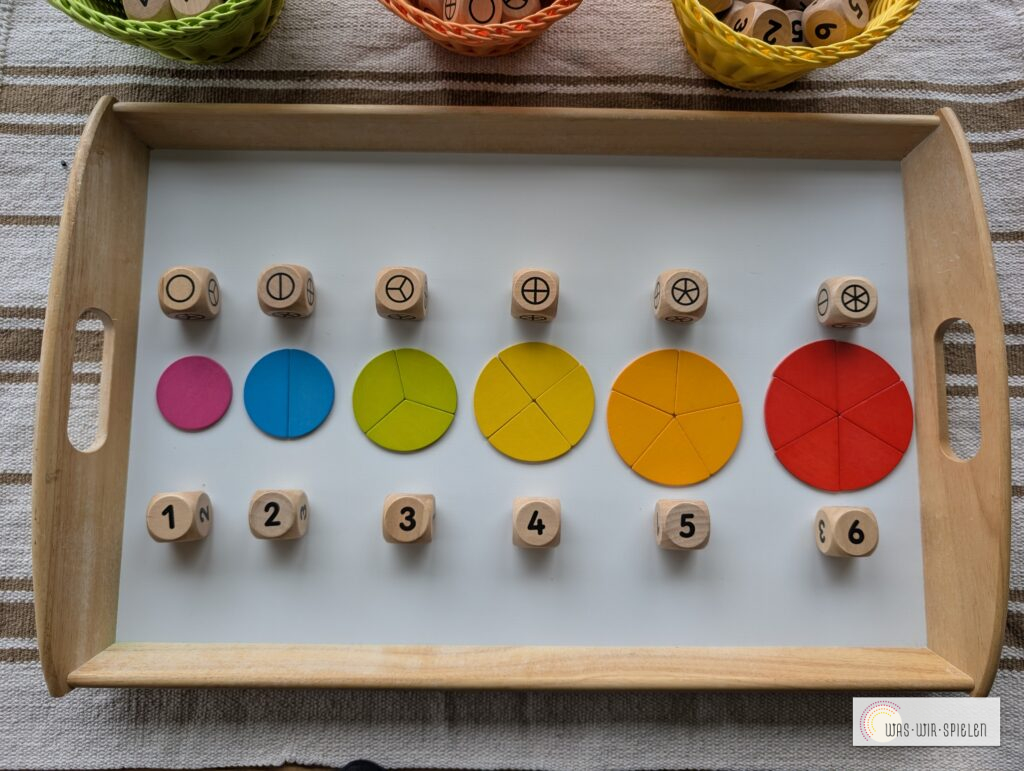
Sie können mit den einzelnen Teilen experimentieren, Ähnlichkeiten herausfinden (drei Sechstel = ein Halbes,…) und durch Spiele ihr Wissen vertiefen.

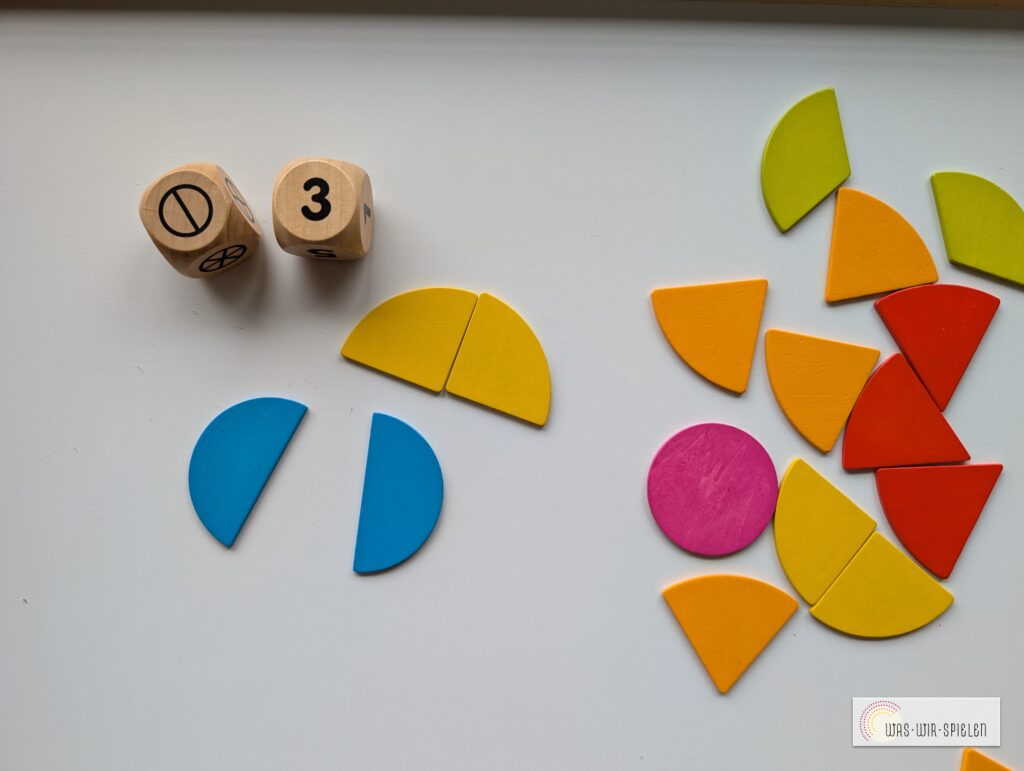
Würfelspiel: das Kind würfelt mit einem Zahlenwürfel und mit einem Bruchwürfel und legt die passenden Teile auf bzw. zeichnet sie auf.

Der Übergang vom Ganzen zu Bruchteilen

Mit verschiedenen Aufgabenstellungen und Fragen kann man das Thema vertiefen. Und auch hier hilft das Material von Höller Spiel, um die einzelnen Aufgaben optisch darzustellen und somit besser im Gedächtnis abspeichern zu können.

Zum Beispiel: 1 Ganzes sind 8 Pizzastücke -> wir haben also 8 Achtel, wenn jemand ein Stück isst, wie viele Achtel haben wir noch? Usw.

In dieser Phase kann man nun auch einzelne Brüche vergleichen und überlegen, welche Teile größer bzw. kleiner sind. Dazu nutze ich gern die Rechenzeichenwürfel mit dem, „Größer als“ und „Kleiner als“ – Zeichen.

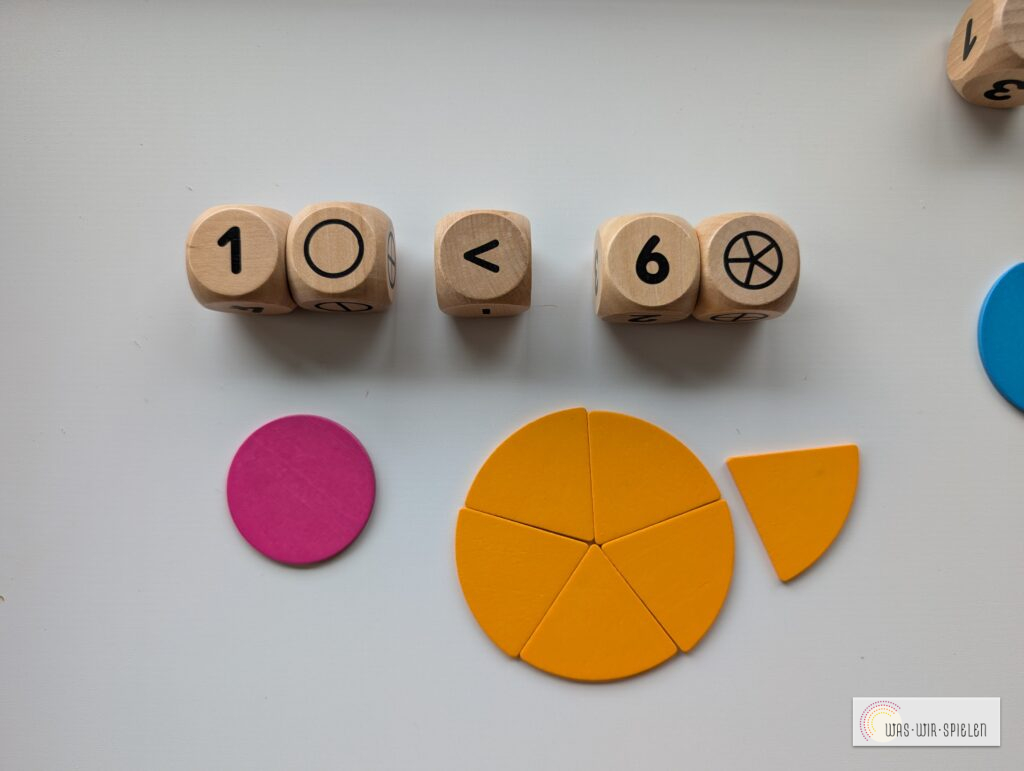
Brüche aufschreiben, vergleichen und damit Rechnen

Beim Aufschreiben der Brüche sind die Bruchwürfel für mich DIE Hilfestellung, damit Kinder das System mit Zählen und Nenner verstehen. Oben liegt immer ein Ziffernwürfel und unten ein Bruchwürfel. So verstehen die Kinder ganz leicht, dass der untere Bruchwürfel, also der Nenner, die Bruchstücke anzeigt (also Achtel, Viertel, Drittel, usw.) und der obere Zahlenwürfel gibt die Anzahl an ( zwei Achtel, 5 Achtel, usw.).

Haben die Kinder dieses System verstanden, wird es für sie ganz logisch sein, dass man beim Rechnen mit Brüchen oder beim Vergleichen von Brüchen diese zuerst auf denselben Nenner bringen muss. Der Bruchwürfel muss gleich sein! Erst dann kann man vergleichen bzw. addieren oder subtrahieren.

Fazit

Das Lernen des Bruchrechnens ist ein entscheidender Schritt in der mathematischen Bildung eines Kindes. Es legt den Grundstein für viele zukünftige mathematische Konzepte und stärkt das Verständnis für Zahlen und ihre Teilbarkeit. Durch den Einsatz von Alltagsbeispielen und regelmäßigem Üben anhand vielseitiger Aufgabenstellungen wird dieses Thema gut verinnerlicht und verstanden. Das Buchrechnungs-Set von Höller Spiel ist für mich DAS perfekte Hilfsmittel um die Thematik visuell verständlich dazustellen und haptisch zu verinnerlichen.

Ich wünsche euch viel Erfolg mit den Brüchen! Wir lesen uns bald wieder!

Liebe Grüße Sandra